Ap stats units 1-5 review – Embark on an in-depth journey through AP Stats Units 1-5 with this comprehensive review. This guide will unravel the intricacies of statistical analysis, equipping you with the knowledge and skills to conquer any data-driven challenge.
From understanding descriptive statistics to mastering hypothesis testing, this review covers all the essential concepts in a clear and engaging manner. Dive into the world of probability, random variables, and confidence intervals, and emerge as a statistical powerhouse.
Descriptive Statistics: Ap Stats Units 1-5 Review
Descriptive statistics provide a concise summary of data, helping us understand its central tendencies and variability. These statistics include measures of central tendency (mean, median, mode) and measures of dispersion (range, variance, standard deviation).
Measures of Central Tendency
- Mean:The average of all data points, calculated by adding them up and dividing by the total number of points. It is sensitive to outliers.
- Median:The middle value when the data is arranged in order from smallest to largest. It is not affected by outliers.
- Mode:The value that occurs most frequently in the data.
Measures of Dispersion
- Range:The difference between the maximum and minimum values in the data.
- Variance:A measure of how spread out the data is from the mean, calculated by finding the average of the squared differences between each data point and the mean.
- Standard Deviation:The square root of the variance, which represents the typical distance of data points from the mean.
Real-World Examples, Ap stats units 1-5 review
Descriptive statistics are used in various fields to analyze data and make informed decisions. For instance, in healthcare, mean and standard deviation can describe the distribution of patients’ blood pressure readings, providing insights into overall health and variability.
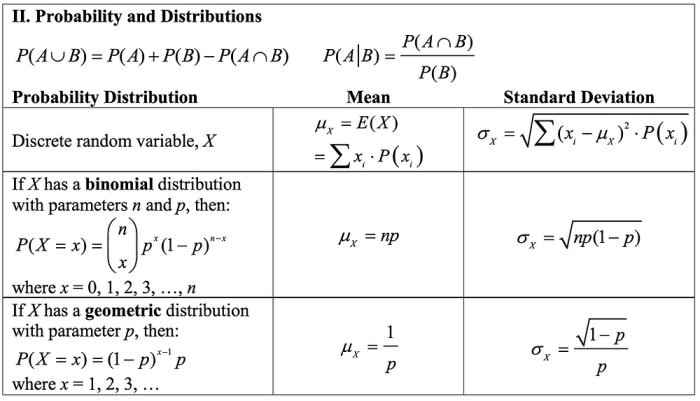
Probability
Probability is the branch of mathematics that deals with the likelihood of events occurring. It is used in many fields, such as statistics, finance, and engineering.The basic concepts of probability include:
- Sample space:The set of all possible outcomes of an experiment.
- Event:A subset of the sample space.
- Probability distribution:A function that assigns a probability to each event in the sample space.
The rules of probability include:
- Addition rule:The probability of the union of two events is the sum of the probabilities of each event.
- Multiplication rule:The probability of the intersection of two events is the product of the probabilities of each event.
Probability distributions are used to describe the likelihood of different outcomes occurring. The most common probability distributions include:
- Binomial distribution:Used to model the number of successes in a sequence of independent experiments.
- Normal distribution:Used to model continuous data that is bell-shaped.
- Poisson distribution:Used to model the number of events that occur in a fixed interval of time or space.
Random Variables
Random variables are functions that assign a numerical value to each outcome of a random experiment. They play a crucial role in probability and statistics, allowing us to describe and analyze the outcomes of random processes.
It’s time to buckle down and review those AP Stats units 1-5 concepts. Need a quick break? Check out this article on maletas / ser / pasajero for a fun distraction. Then, come right back to crush those review questions and ace your upcoming AP Stats exam!
A random variable has several key properties:
- Outcome Space:The set of all possible outcomes of the random experiment.
- Sample Space:The set of all possible values that the random variable can take.
- Probability Distribution:The function that assigns probabilities to each value in the sample space.
Types of Random Variables
Random variables can be classified into two main types:
- Discrete Random Variables:Take on a finite or countable number of distinct values.
- Continuous Random Variables:Take on any value within a specified range.
Discrete random variables can be further classified into:
- Binomial:Counts the number of successes in a sequence of independent experiments.
- Poisson:Counts the number of events occurring within a fixed interval of time or space.
- Geometric:Counts the number of trials until the first success in a sequence of independent experiments.
Continuous random variables can be further classified into:
- Uniform:Takes on any value within a specified range with equal probability.
- Normal (Gaussian):Takes on values that are symmetrically distributed around a mean.
- Exponential:Takes on values that decrease exponentially as they move away from a minimum.
Hypothesis Testing
Hypothesis testing is a statistical method used to determine whether a particular hypothesis about a population parameter is supported by the available evidence. It involves comparing a sample statistic to a hypothesized value to assess the likelihood of obtaining the observed results if the hypothesis is true.
Steps Involved in Hypothesis Testing
The steps involved in hypothesis testing include:
- Formulating the null and alternative hypotheses
- Collecting data
- Calculating the test statistic
- Determining the p-value
- Making a decision
Types of Hypothesis Tests
There are different types of hypothesis tests, each designed for specific situations. Some common types include:
- One-sample t-tests: Used to test whether the mean of a population is equal to a hypothesized value.
- Two-sample t-tests: Used to test whether the means of two populations are equal.
Confidence Intervals
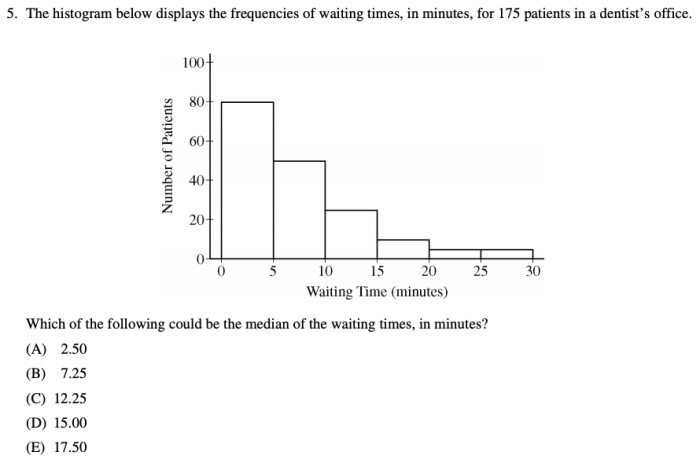
Confidence intervals are a way to estimate the true value of a population parameter, such as a mean or a proportion. They are based on the idea that we can use a sample to make inferences about the population from which it was drawn.
There are different types of confidence intervals, depending on the parameter being estimated. For example, confidence intervals for means are used to estimate the true mean of a population, while confidence intervals for proportions are used to estimate the true proportion of a population that has a certain characteristic.
Calculating Confidence Intervals
The formula for calculating a confidence interval is:
sample estimate ± margin of error
The sample estimate is the point estimate of the population parameter, such as the sample mean or sample proportion.
The margin of error is a measure of the amount of error that is allowed in the estimate. It is calculated using the sample size, the standard deviation of the sample, and the desired level of confidence.
Interpretation of Confidence Intervals
Confidence intervals are interpreted as follows:
- The lower bound of the confidence interval is the smallest value that the population parameter could be, given the sample data and the desired level of confidence.
- The upper bound of the confidence interval is the largest value that the population parameter could be, given the sample data and the desired level of confidence.
- The width of the confidence interval is a measure of the precision of the estimate. A narrower confidence interval indicates a more precise estimate.
General Inquiries
What is the purpose of descriptive statistics?
Descriptive statistics provide a concise summary of data, allowing us to understand its central tendencies and variability.
How is probability used in real-world scenarios?
Probability plays a crucial role in decision-making, risk assessment, and predicting future outcomes.
What are the different types of random variables?
Random variables can be classified as discrete or continuous, depending on whether they can take on a finite or infinite number of values.
What is the importance of hypothesis testing?
Hypothesis testing allows us to make inferences about a population based on sample data, helping us to draw conclusions and make informed decisions.
How are confidence intervals used in statistical analysis?
Confidence intervals provide a range of values within which we can be confident that the true population parameter lies.